Perfect gas adiabatic expansion

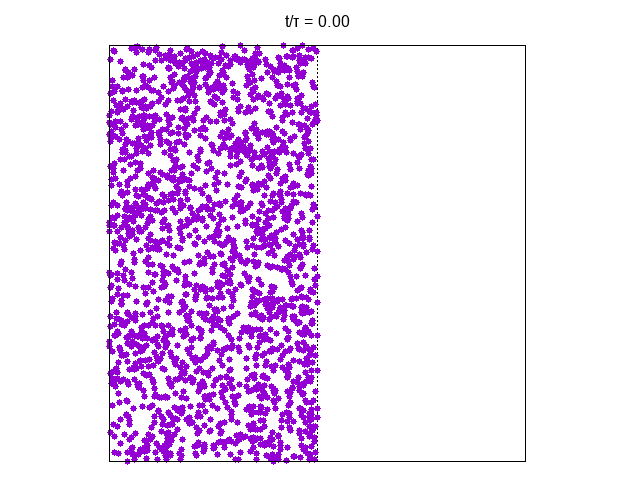
We here make the example of a perfect gas bounded on a 2d square box with perfectly reflecting walls. We consider initial states where velocity of each particle is thermalised i.e. is a random variable taken from Mawell distribution. The temperature $T$ gives the variance of the gaussian distribution given unitary mass for any particle. The lenght of the box $L$ is also taken as unit length.

A natural measure for time is the time it take a particle with speed $v=\sqrt{<v^2>}=\sqrt{T}$ to travel for a length $L$ $\tau = L/v$ the ballistic time-scale.

The distribution for position can be obtained analytically trough the procedure described in this paper. We hereby show some results that can be obtained by tracking the trajectory of any particle.

time evolution

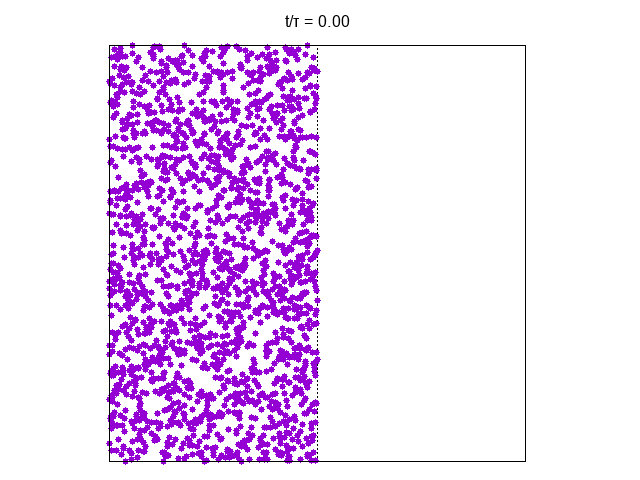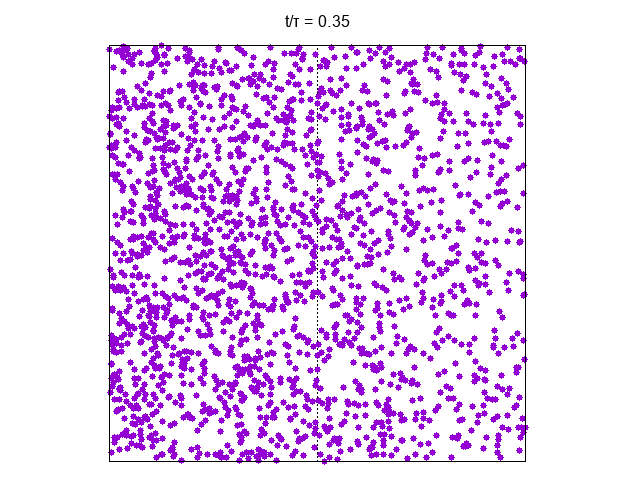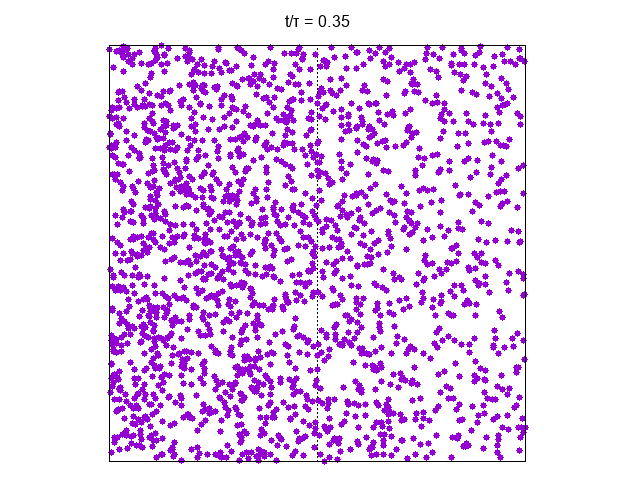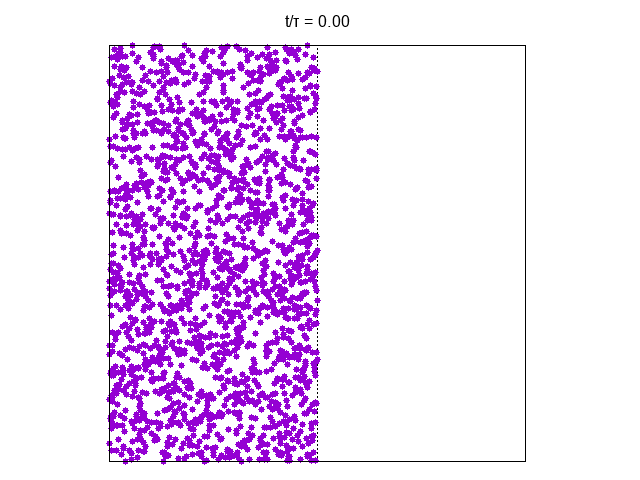
We can consider the gas initially confined to the right part of the vessel as in the figure

On a time-scale of the order of $\tau$ the gas will invade the available space

equilibration

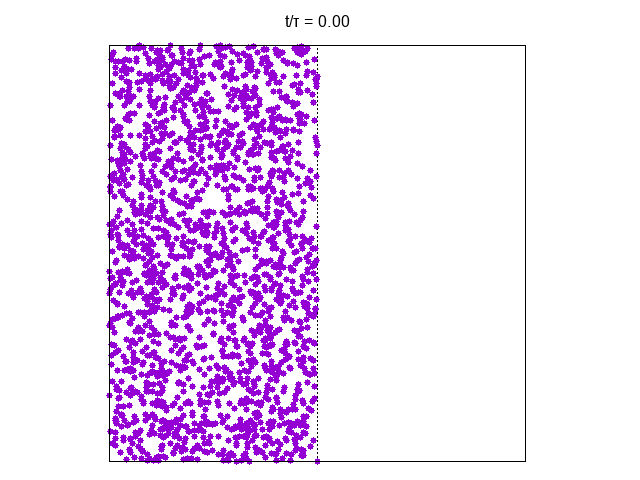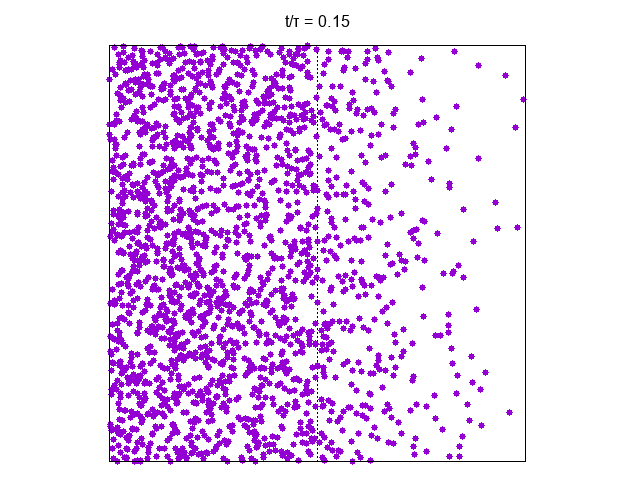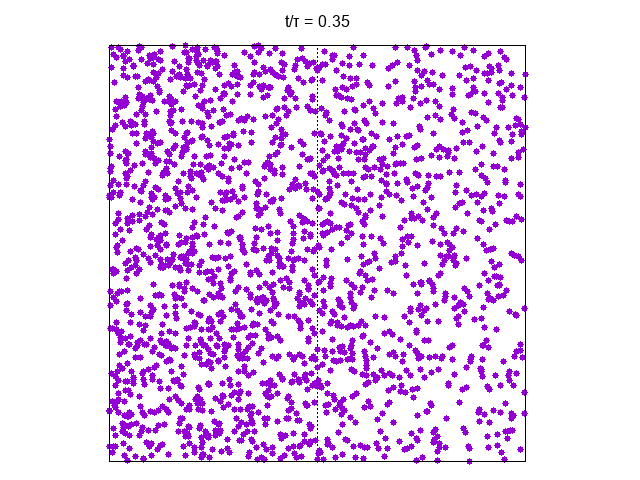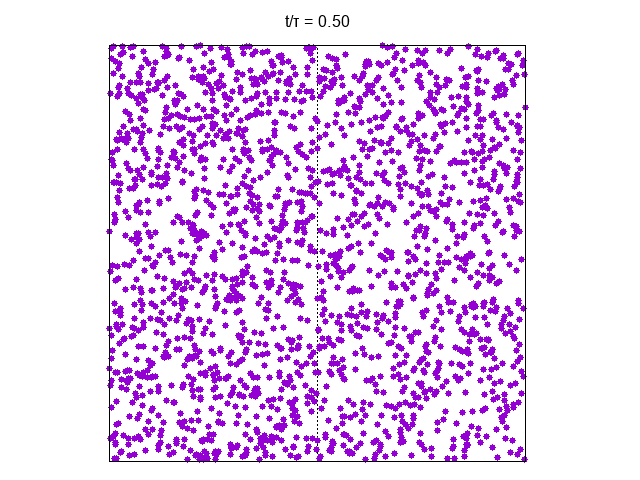
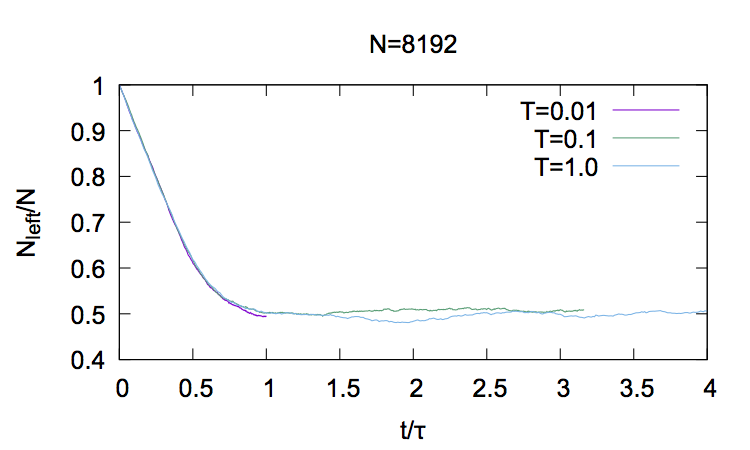
That the temperature dependent time-scale $\tau$ is the time-scale needed for “equilibration” of position is shown in the following picture where the total number of the particles in the left part of the vessel is shown as a function of $t/\tau$ for several temperatures

time reversal

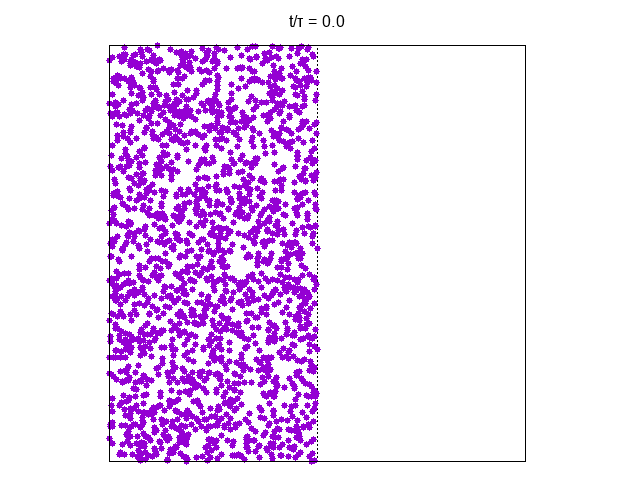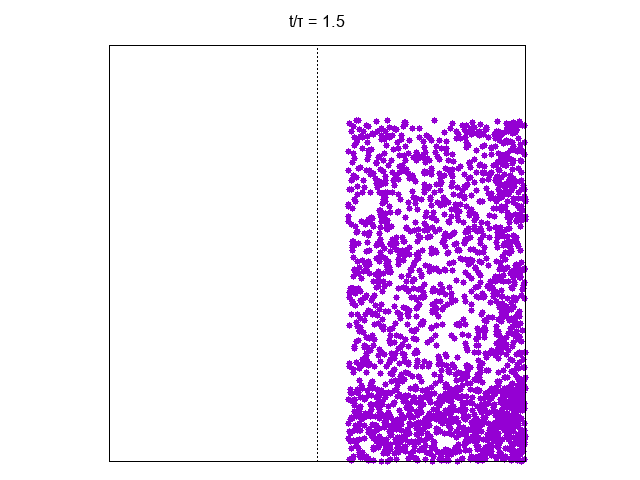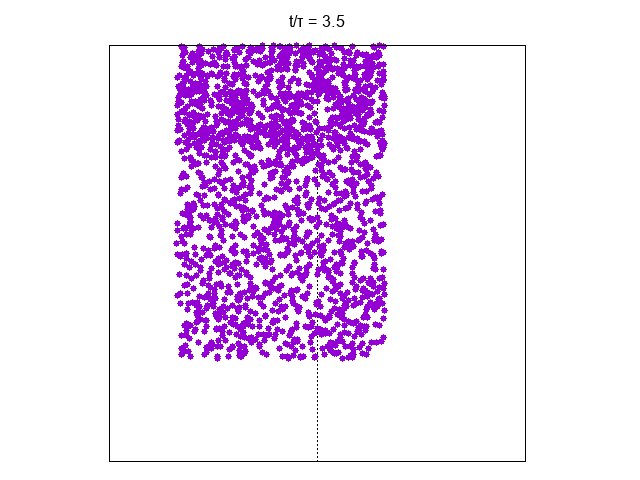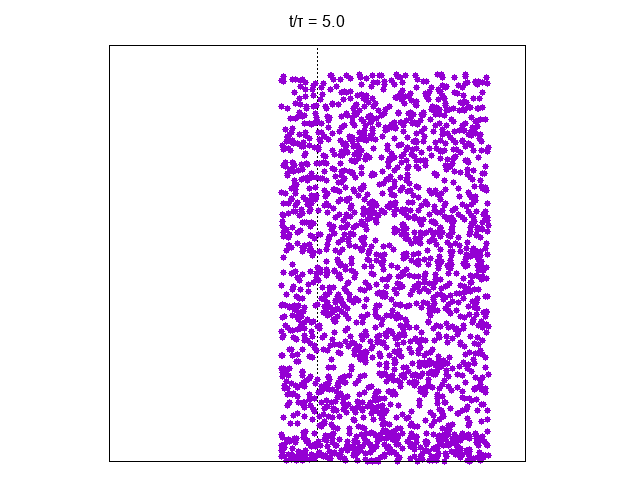
It is interesting to show explicitly the Loschmidt paradox by inverting the partcles’ velocity at a given time (here $t_{rev}=\tau/2$)

velocity relaxation

In the perfect-gas model there is no velocity relaxation. Due to elastic scattering with the walls the modulus of velocity of any particle is fixed and a very unlikely initial configuration for velocity does not equilibrate. Here all the particles have the initial velocity $v=(0.617667824838856,0.786439100095383)$

Loschmidt paradox

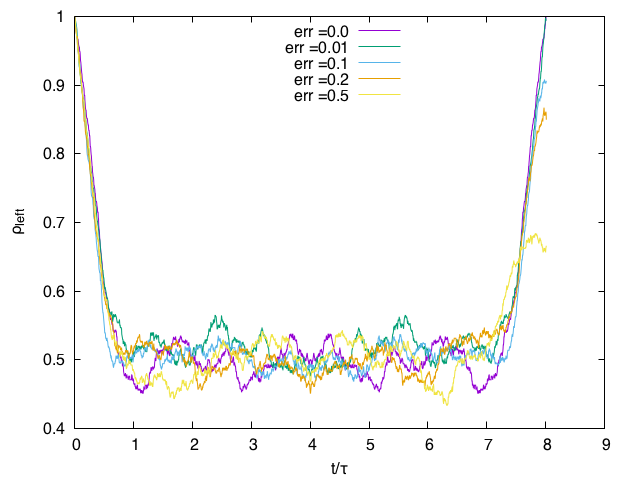
The absence of interactions imply absence of chaos. Hence a small error in the reversal procedure do not imply catastrophyc consequences for time-reversal, this is shown in the following plot where the density in the left part of the vessel is shown as a function of the scaled time for various errors in the velocity reversal where the error err appears in the velocity reversal as

and $r$ is a random number $[-1/2:1/2]$.

Work on it!

The previous statement and many other can be checked by peforming the time evolution by yourself. A simple code written in gnuplot gives the momentum and position of one particle in one dimension. Here $t$ is time $x0$ $p0$ are initial position and momentum

#################################
#
# 1-d particle within perfectly reflecting walls [-L/2:L/2]
#
L=1.0
#
k(t,x0,p0)=int(t*abs(p0)/L+1./2.+sgn(p0)*x0/L)
#
# momentum
#
p(t,x0,p0)=p0*(-1)**k(t,x0,p0)
#
# position
#
x(t,x0,p0)=(x0+p0*(t-k(t,x0,p0)*L/abs(p0)))*(-1)**k(t,x0,p0)
#
#################################

For the perfect gas this is sufficient to integrate the system in any dimension without any integration error but numerical rounding.