a) Prove that for a translational invariant potential $V(\vec{x}-\vec{y})$ the second quantization expression

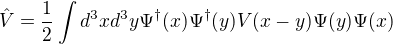
is equivalent to

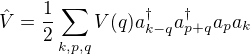
Use the plane wave expansion of $\Psi$ where $u_k(x)=\frac{1}{\sqrt{V}}\exp i k x$ and $V$ is the volume. Note that all indexes are vectorial and the spatial dimension is 3.

b) Prove that the equilibrium single-particle density matrix for a free particle is

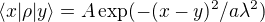
where $\lambda$ is the De Broglie wavelength. Find the normalization $A$ for a tree dimensional space and the numerical coefficient $a$. Comment the results. Compare the result for $\langle x| \rho |y \rangle$ to that for $\langle p| \rho |p^\prime \rangle$ with $p$ and $p^\prime$ are three dimensional wave vectors.

c) Consider a perfect gas of massless ultrarelativistic bosonic or fermionic particles $\epsilon(p)=c p$. When the total number of particle is not conserved then $\mu=0$. In this case find the equation of state i.e. the dependence of pressure by volume if any, draw qualitatively some isotherms and compare with the number-conserved ultrarelativistic fermionic case at $T=0$.