due date: 10 Jan 2021

a) Redo exercise #4 if you dont succeed to answer to some points in the previous homework session.

b) Consider the perfect Fermi and Bose gas with a general single particle dispersion $\epsilon(p)= a |p|^b$. Determine:

c) Consider a perfect gas of bosonic non-relativistic particles in $d$ dimensions. Discuss the existence of Bose-Einstein condensation as a function of the system dimensionality. Using the relation $PV=2 U/3$ prove that when $T<T_{BE}$ the pressure depends only on temperature and find its temperature dependence.

d) Prove that the equilibrium single-particle density matrix

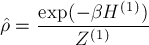
for a free particle is

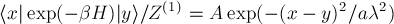
where $Z^{(1)}$ is the single particle partition function, $\lambda$ is the De Broglie wavelength and $|x>,|y>$ position eigenstates. Find the normalization $A$ for a tree dimensional space and the numerical coefficient $a$. Comment the results. Compare the result for $\langle x| \rho |y \rangle$ to that for $\langle p| \rho |p^\prime \rangle$ with $p$ and $p^\prime$ are three dimensional wave vectors.

e) A team of 12 reindeers pull the sleigh of QuantaClaus. Assume that (notwithstanding his belly) Quanta is a pointlike particle as well as the reindeers (which, as you know, can be safely approximated by spherical cows with zero radius). Write a Hamiltonian for the system in second quantisation and consider spinless reindeers.