Exercise #1
due date: October 24 2022
a) Consider the following thermodynamic cycle for a perfect gas:
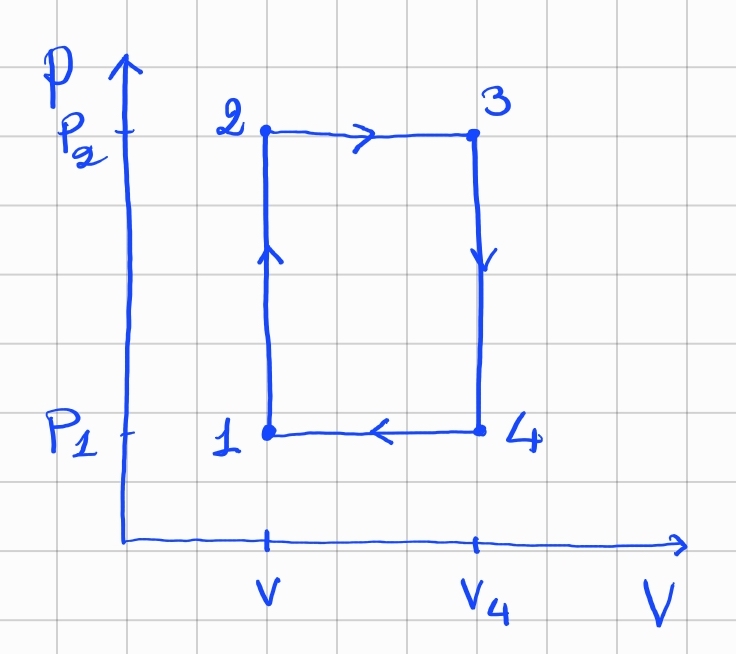
-
Draw the cycle in the T-S plane.
-
Calculate the total work exerted by the system (W).
-
Calculate the total heat exchanged by the system (Q).
-
Calculate the efficiency $\eta={W}/{Q_{abs}}$ where $Q_{abs}$ is the absorbed heat.
In the following you can alternatively choose b1) or b2).
b1) Read the notes about the Kac ring model:
-
which set of variables describes a microscopic state?
-
which set of variables describes the macroscopic state?
-
write a code to calculate the number of black and white point (you can also do it considering a small size say N=4 and doing the evolution by hand…)
-
compare the output of the code with the "molecular-chaos" solution given in the notes and discuss the results.
b2) Read the notes about the Logistic map:
-
write a code to calculate the map evolution and the Lyapunov exponent.
-
discuss the results in the parameters space described in the note discussing the local stability and the Lyapunov exponent.
-
When the system is chaotic the time average of $y$ converge to a time-independent value? Is this value independent on initial data?
c1) Consider only one one-dimensional classical harmonic oscillator
-
write the Hamilton equation and plot a typical trajectory in the phase space
-
is the system chaotic?
c2) now consider an ensemble made of replicas of the previous case i.e. one-dimensional classical harmonic oscillator with same $\omega$ and mass
-
write the Liouville’s evolution for and ensemble of such systems using momenta and position as variables
-
consider an isoenergetic ensemble of oscillators (all osc. have energy=E). This ensemble starts with random phases between $\phi_0$ and $\phi_0+\Delta$. In such conditions evaluate $<x(t)>$. Does it tends to a constant value? Is the system ergodic? Is the system mixing?