1. Exercise #1
due date: October 24 2022
a) Consider the following thermodynamic cycle for a perfect gas:
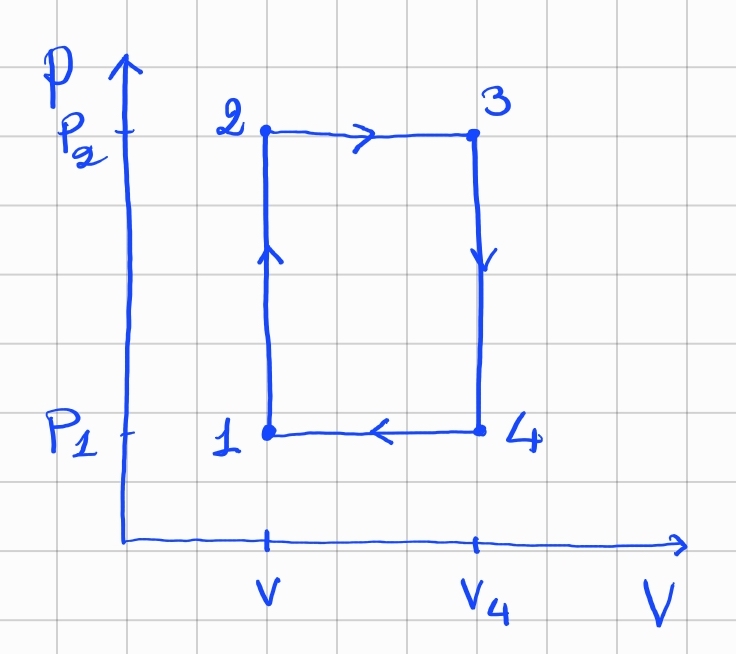
-
Draw the cycle in the T-S plane.
-
Calculate the total work exerted by the system (W).
-
Calculate the total heat exchanged by the system (Q).
-
Calculate the efficiency $\eta={W}/{Q_{abs}}$ where $Q_{abs}$ is the absorbed heat.
In the following you can alternatively choose b1) or b2).
b1) Read the notes about the Kac ring model:
-
which set of variables describes a microscopic state?
-
which set of variables describes the macroscopic state?
-
write a code to calculate the number of black and white point (you can also do it considering a small size say N=4 and doing the evolution by hand…)
-
compare the output of the code with the "molecular-chaos" solution given in the notes and discuss the results.
b2) Read the notes about the Logistic map:
-
write a code to calculate the map evolution and the Lyapunov exponent.
-
discuss the results in the parameters space described in the note discussing the local stability and the Lyapunov exponent.
-
When the system is chaotic the time average of $y$ converge to a time-independent value? Is this value independent on initial data?
c1) Consider only one one-dimensional classical harmonic oscillator
-
write the Hamilton equation and plot a typical trajectory in the phase space
-
is the system chaotic?
c2) now consider an ensemble made of replicas of the previous case i.e. one-dimensional classical harmonic oscillator with same $\omega$ and mass
-
write the Liouville’s evolution for and ensemble of such systems using momenta and position as variables
-
consider an isoenergetic ensemble of oscillators (all osc. have energy=E). This ensemble starts with random phases between $\phi_0$ and $\phi_0+\Delta$. In such conditions evaluate $<x(t)>$. Does it tends to a constant value? Is the system ergodic? Is the system mixing?
| NAME | ID | a) | b) | c1) | c2) |
|---|---|---|---|---|---|
- |
SM01 |
A- |
B- |
B- |
A- |
- |
SM02 |
A- |
C- |
C |
D |
- |
SM03 |
A- |
B- |
C |
D- |
- |
SM04 |
C- |
D |
D |
- |
- |
SM05 |
A- |
C- |
D |
C |
- |
SM06 |
A |
C |
B |
A- |
- |
SM07 |
B- |
E |
D |
A- |
- |
SM08 |
A- |
D |
C+ |
B |
- (D) |
SM09 |
D |
? |
D |
C- |
- (D) |
SM10 |
B |
C- |
C |
D |
2. Exercise #2
due date: November 7 2022
a) Consider N classical independent one-dimensional harmonic oscillators (mass $m_i$, frequency $\omega_i$ $i=1,N$) whose initial data are taken according Boltzmann distribution for position and momenta at temperature $T$. Let them evolve and calculate the following correlation functions:
$C_{i,j}(t,t')=< p_i(t)p_j(t') >$, $G_{i,j}(t,t')=< x_i(t)x_j(t') >$ where averages are taken on the Boltzmann distribution of initial data.
By assuming a distribution of the oscillator’s frequencies ($\omega_i>0$) $P(\omega)\propto \omega^2 \;\;\; \omega<\Lambda$ as well as equal masses for all oscillators calculate in the large $N$ limit:
$C(t,t')=(1/N)\sum_{i,j} C_{i,j}(t,t')$, $G(t,t')=(1/N)\sum_{i,j} G_{i,j}(t,t')$
find the time evolution of these functions, temperature dependence and dependence on the cutoff $\Lambda$.
hint(1) : express the solution for x and p as a function of initial data $x(0)$ and $p(0)$.
hint(2) : express the solution for x and p as a function of amplitude an phase and then express the Boltzmann distribution in the same variables.
b1) Read the notes. Show the the interaction-dependent term $\hat{L}$ defined in page 8 is hermitian.
b2) optional Consider the generalised Gauss theorem and show that if $\rho(x)=\Delta_\Omega (x)$ is the characteristic function of the set $\Omega$ the the standard Gauss theorem follows.
c) Consider the BBGKY evolution equation for the reduced ensemble density of a classical system in the case of non interacting particles but in the presence of an external potential $\Phi(\vec{q})$.
Make the hypotesis that velocities are thermalised such that the one particle distribution can be written as
Demonstrate that the equilibrium distribution for the positional part is
ò$u^{(1)}(\vec{q})\propto \exp [-\beta \Phi(\vec{q}) $ ]
d) Read the chapter 3 of the textbook (Kerson Huang, "Statistical Mechanics", Second Edition, Wiley). Try to answer to one of the problems of the chapter at your convenience. If you dare you can try exercise 3.5 and for that it would be useful to read this paper
| NAME | ID | a) | b1) | b1) | c) | d) |
|---|---|---|---|---|---|---|
- |
SM01 |
A |
A |
A |
C |
B |
- |
SM02 |
B |
A |
- |
C |
B |
- |
SM03 |
B |
A |
- |
C |
B |
- |
SM04 |
- |
- |
- |
- |
- |
- |
SM05 |
B |
A |
- |
C |
B |
- |
SM06 |
B |
A |
- |
A |
B+ |
- |
SM07 |
B |
A |
- |
C |
D |
- |
SM08 |
A |
A |
- |
B |
B |
- |
SM09 |
B |
A |
- |
C |
C |
- |
SM10 |
B |
A |
- |
C |
B+ |
3. Exercise #3
due date: December 4th 2022
a) Following the lines of the notes derive the statistical properties of the noise term $\xi(t)$ as a result of the equilibrium distribution for the oscillators. Perform explicitly the $N\rightarrow \infty$ limit using the Ohmic spectral density. Does the noise correlation function behaviour depends on the $\omega\rightarrow 0$ behviour of the spectral density? You can optionally answer to this question trying to guess a spectral density which goes as $\omega^\alpha$ for small $\omega$.
b) Consider the stochastic equation for the moment of a particle under the action of external random forces $\xi(t)$ (in one dimension):
$\dot{p}(t)=-\gamma p(t) + \xi(t)$
where
$\langle \xi(t) \rangle = 0$
$\langle \xi(t) \xi(t')\rangle = 2 M \gamma k_b T \delta(t-t')$
-
Derive without approximation the average mean square displacement
$\Delta(t)=\langle |x(t)-x(0)|^2 \rangle$
-
Derive the behaviour of $\Delta(t)$ for large and small times and define the time scale above which the behaviour of $\Delta(t)$ is linear in time.
c) Consider the Fokker-Planck equation in one dimension
$\frac{\partial}{\partial t} P(x,t) = \frac{\partial}{\partial x} F(x)P(x,t) +\frac {\epsilon}{2}\frac{\partial^2}{\partial x^2} P(x,t)$
following the lines of the notes
show that for a potential problem
$F(x) = -\frac{\partial}{\partial x} V(x)$
the stationary distribution is given by
$P(x)=\exp(-2V(x)/\epsilon)$.
Consider the multidimensional Fokker-Plank equation and derive the equation for position and momenta in the case of a particle moving in one dimension under the action of a potential force. Comment the equation and compare it with the Boltzmann equation.
Derive the Maxwell Boltzmann distribution as stationary joint distribution momenta and of the position.
d) A polymer can be constructed as a three dimensional random walk where the position of the n+1-th monomer is given by
$\vec{r}_{n+1}=\vec{r}_{n}+a\hat{u}_{n+1}$
where $a$ is the monomer spacing and $\hat{u}$ is a random unit vector. The length of the polymer made by $N+1$ monomers can be estimated by
$\ell= \sqrt{\langle |\vec{r}_{N}-\vec{r}_{0}|^2 \rangle}}$
where the average is taken over the random orientation of the unit vectors $\hat{u}_n$.
-
Calculate the ratio $\ell/Na$ and comment the result.
| NAME | ID | a) | b) | c) | d) |
|---|---|---|---|---|---|
- |
SM01 |
A |
A |
A |
D |
- |
SM02 |
B+ |
A- |
C |
D |
- |
SM03 |
B+ |
A- |
C |
D |
- |
SM04 |
- |
- |
- |
- |
- |
SM05 |
B+ |
A |
A- |
A |
- |
SM06 |
A+ |
A |
A+ |
D |
- |
SM07 |
- |
- |
- |
- |
- |
SM08 |
A+ |
A |
A+ |
D |
- (D) |
SM09 |
A+ |
A |
C |
D |
- |
SM10 |
A+ |
B |
A+ |
A |
4. Exercise #4
due date: December 19th 2022
a) Consider a classical perfect gas and calculate the entropy in the canonical ensemble. Compare the result with that given, in the microcanonical ensemble, by the Sackur-Tetrode formula and show the ensemble equivalence in the thermodynamic limit.
b) Consider the following Hamiltonian for $N$ independent spin $\sigma=\pm 1$
$H=-gB\sum_i \sigma_i$
Where $B$ is the external magnetic field along $z$, $g$ a coupling constant and $\sigma_i$ the Pauli matrix $\sigma_z$ at a given site $i$. Spin operators at different sites commute.
Perform the calculation in the microcanonical ensemble at fixed total energy, calculate the entropy. Plot the dimensionless entropy per spin ($S/k_B N$) as a function of a suitably defined dimensionless energy.
Perform the calculation of the entropy in the canonical ensemble at fixed total temperature.
Compare the results of the previous two points by expressing the canonical entropy as a function of the internal energy.
Comment the result.
c) In the grandcanonical ensemble calculate the dimensionless ratio $\beta P/\rho$ where $\rho=N/V$ is the number density by performing a fugacity expansion in $z=\exp(\beta\mu)$ up to second order in $z$.
Perform the calculation in the case of an interacting classical gas with pair interactions.
Perform the calculation in the case of a quantum perfect gas in the case of Fermi-Dirac and Bose-Einstein statistics.
Express the result in term of the number density in both cases. Comment the two results.
d) Consider two one particle states made by one-dimensional gaussians
$g_1(x)=A\left ( \exp(-\frac{(x-x_0)}{2\sigma^2}) \right)^{1/2}$
$g_2(x)=A\left ( \exp(-\frac{(x+x_0)}{2\sigma^2}) \right)^{1/2}$
with $A$ being a normalisation constant. Using these states write a possible state for 2 fermions and 2 bosons in state $1$ or $2$ neglecting the spin component. Calculate the average distance $\langle | x_1-x_2 | ^2 \rangle$ as a function of $x_0$ (you can choose $\sigma^2=1$). Comment the results.
| NAME | ID | a) | b) | c) | d) |
|---|---|---|---|---|---|
- |
SM01 |
A |
C |
C+ |
C |
- |
SM02 |
A |
D |
D |
C |
- |
SM03 |
A |
C |
D |
A- |
- |
SM04 |
- |
- |
- |
- |
- |
SM05 |
A |
B |
B |
C+ |
- |
SM06 |
A |
C+ |
B |
A- |
- |
SM07 |
- |
- |
- |
- |
- |
SM08 |
A |
C |
A |
A- |
- |
SM09 |
A |
C |
D |
C+ |
- |
SM10 |
A |
C- |
C |
C |