Exercise #1
due date: October 23 2023
a) Consider the following thermodynamic cycle for a perfect gas:
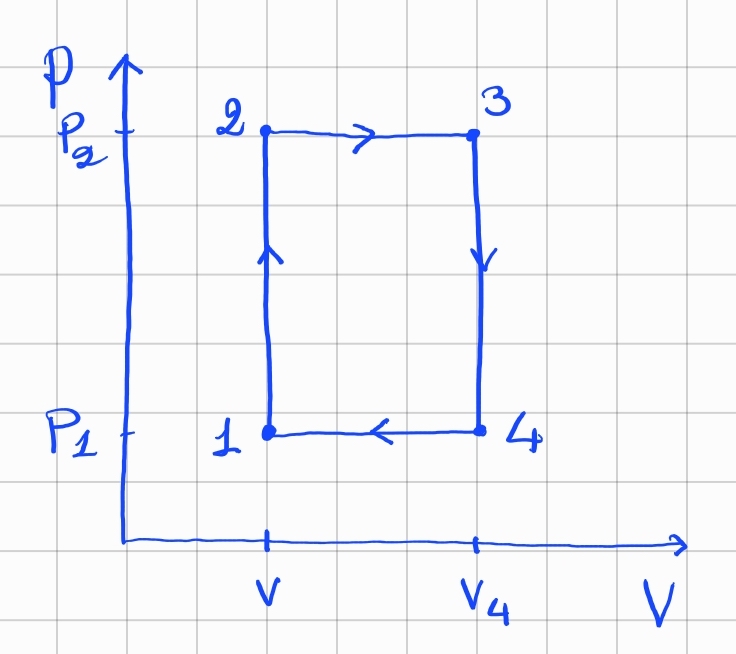
-
Draw the cycle in the T-S plane.
-
Calculate the total work exerted by the system (W).
-
Calculate the total heat exchanged by the system (Q).
-
b) Consider only one one-dimensional classical harmonic oscillator
-
write the Hamilton equation and plot a typical trajectory in the phase space
now consider an ensemble made of replicas of the previous case i.e. one-dimensional classical harmonic oscillator with same $\omega$ and mass
-
write the Liouville’s evolution for and ensemble of such systems using momenta and position as variables
-
consider an isoenergetic ensemble of oscillators (all osc. have energy=E). This ensemble starts with random phases between $\phi_0$ and $\phi_0+\Delta$. In such conditions evaluate $<x(t)>$. Does it tends to a constant value?
c) Consider a classical perfect gas and calculate the entropy in the canonical ensemble. Compare the result with that given, in the microcanonical ensemble, by the Sackur-Tetrode formula and show the ensemble equivalence in the thermodynamic limit.
d) Consider the following Hamiltonian for $N$ independent spin $\sigma=\pm 1$
$H=-gB\sum_i \sigma_i$
Where $B$ is the external magnetic field along $z$, $g$ a coupling constant and $\sigma_i$ the Pauli matrix $\sigma_z$ at a given site $i$. Spin operators at different sites commute.
Perform the calculation in the microcanonical ensemble at fixed total energy, calculate the entropy. Plot the dimensionless entropy per spin ($S/k_B N$) as a function of a suitably defined dimensionless energy.
Perform the calculation of the entropy in the canonical ensemble at fixed total temperature.
Compare the results of the previous two points by expressing the canonical entropy as a function of the internal energy.
Comment the result.