due date: November 20th 2023

a) Consider two one particle states made by one-dimensional gaussians

$g_1(x)=A\left ( \exp(-\frac{(x-x_0)^2}{2\sigma^2}) \right)^{1/2}$

$g_2(x)=A\left ( \exp(-\frac{(x+x_0)^2}{2\sigma^2}) \right)^{1/2}$

with $A$ being a normalisation constant. Using these states write a possible state for 2 fermions and 2 bosons in state $1$ or $2$ neglecting the spin component. Calculate the average distance $\langle | x_1-x_2 | ^2 \rangle$ as a function of $x_0$ (you can choose $\sigma^2=1$). Comment the results.

b) Consider the perfect Fermi and Bose gas with a general single particle dispersion $\epsilon(p)= a |p|^b$. Determine:

c) Consider a perfect gas of bosonic ultra-relativistic particles in 3 dimensions with vanishing chemical potential (black body). Calculate internal energy as a function of temperature and using the relation derived in the previous point prove that the radiation pressure is independent of volume and is proportional to $T^4$.

d1) Prove that the equilibrium single-particle density matrix for Boltzmann particle is

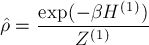
for a free particle is

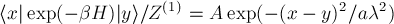
where $Z^{(1)}$ is the single particle partition function, $\lambda$ is the De Broglie wavelength and $|x>,|y>$ position eigenstates (in 3 dimensions). Find the normalization $A$ for a tree dimensional space and the numerical coefficient $a$. Comment the results. Compare the result for $\langle x| \rho |y \rangle$ to that for $\langle p| \rho |p^\prime \rangle$ with $p$ and $p^\prime$ are three dimensional wave vectors.

d2) Optional Consider the equilibrium single-particle density matrix in the grand-canonical ensemble for massive non-relativistic non-interacting Bose particles. Write its form in momentum and position (3d) representation. Comment the limit $\mu\rightarrow 0^{-}$ for the density matrix in the coordinate representation. Using the fugacity expansion to all order or the integral expression of the density matrix write a code to evaluate numerically it when $\mu < 0$.