Exercise #3
due date: November 26th 2024
a) Consider two one particle states made by one-dimensional gaussians
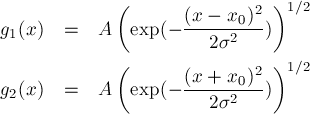
with $A$ being a normalisation constant. Using these states write a possible state for 2 fermions and 2 bosons in state $1$ or $2$ neglecting the spin component. Calculate the average distance < | x1-x2 | 2 > as a function of x0. Comment the results.
b) Consider the perfect Fermi and Bose gas with a general single particle dispersion \epsilon(p)= a |p|b Determine:
-
the density of the states (DOS)
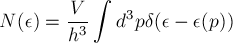
-
the relation between PV and U as a function of the DOS parameters and verify that for massive non relativistic particles either bosonic or fermionic the relation is exactly the same as for Boltzmann’s particles
You can choose between the following c1) and c2)
c1) Consider a perfect gas of bosonic ultra-relativistic particles in 3 dimensions with vanishing chemical potential (black body). Calculate internal energy as a function of temperature and using the relation derived in the previous point prove that the radiation pressure is independent of volume and is proportional to T4.
c2) Following the same lines as done for classical interacting particles perform the fugacity expansion to the second order for quantum perfect gas of fermionic and bosonic particles and comment the results by comparison with classical interacting particles.
d1) Prove that the equilibrium single-particle density matrix for Boltzmann particle
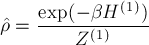
is for a free particle
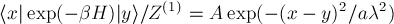
where Z(1) is the single particle partition function, \lambda is the De Broglie wavelength and |x>,|y> position eigenstates (in 3 dimensions). Find the normalization (A) for a tree dimensional space and the numerical coefficient (a). Comment the results. Compare the result for < x| \rho |y > to that for <p1| \rho |p2 > with p1 and p2 are three dimensional wave vectors.
d2) Optional Consider the equilibrium single-particle density matrix in the grand-canonical ensemble for massive non-relativistic non-interacting Bose particles. Write its form in momentum and position (3d) representation. Comment the limit \mu → 0- for the density matrix in the coordinate representation. Using the fugacity expansion to all order or the integral expression of the density matrix write a code to evaluate numerically it when \mu < 0.